Elementary plane geometry construction

1.To bisect a line segment:

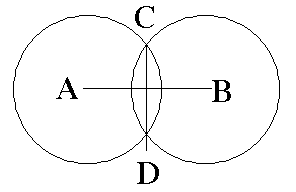
Let AB be the given line segment. With A & B as centers, draw two circles that have the same radius and that intersect each other in two points, C & D. Draw line segment CD.

2.To bisect an angle:

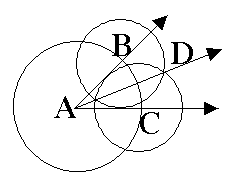
Let < A be the given angle. With A as the center, draw a circle that intersects the sides of the angle in points B & C. With B & C as centers, draw two circles that have the same radius and that intersect each other in point D. Draw AD. This ray bisects the angle.

3.To construct an angle equal in measure to a given angle:

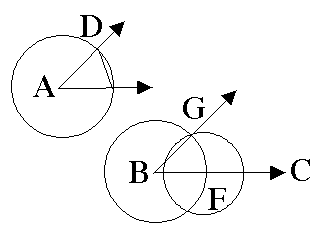
Let < A be the given angle. Draw a ray BC as one side of the angle to be constructed. With A as center, draw a circle that intersects the sides of < A in points D & E. Also draw a circle with the same radius and with B as center that intersects BC in point F. With Fas center and the distance between D & E as radius, draw a circle intersecting the previous one in point G. Draw BC. < B = < A.

4.To construct the reflection of a point through a line:

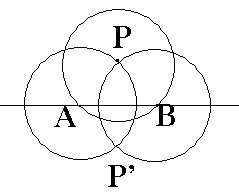
Let the point be P and the line be L. first, with P as center, draw a circle that intersects L in two points, A & B. Then, with A & B as centers, draw two more circles with the same radius as the first one. The circles with centers at A & B intersect in two points: point P and its reflection, point P'.

5.To construct the reflection of a point through a point:

Let P be the point to be reflected through point O. Draw OP. With O as center and OP as radius, draw a circle. The circle intersects line OP in two points: point P and its reflection, point P'.

6.To construct the line perpendicular to a given line though a point on it:

Let U be the given point on the line. With U as center, draw a circle intersecting the line at O & L. Finish the construction by bisecting OL as described above.

7.To construct the line perpendicular to a given line through a point not on it:

Reflect the point M through the line as described above. Draw MM'; MM' is perpendicular to line H.

8.To construct the line parallel to a given line through a point not on it:

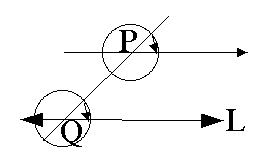
Through a point Q on line L, draw line PQ. With Q as center, draw an arc; repeat with P using the same radius. Measure chord of Q's arc and determine P's cord with this measurement. Draw parallel line PX.

9.To construct the tangents to a circle from a given external point:

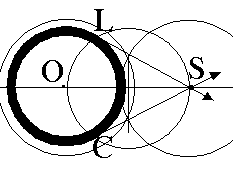
Draw OS. Bisect OS and label its midpoint T. Draw a circle with T as center and TO as radius. Label the two points at which it intersects circle O points C & L. Draw SC and SL. SC and SL are tangent to circle O.

10.To circumscribe a circle about a triangle:

Bisect two of the sides and draw lines perpendicular through each. Using the point of intersection as center and any of the verticies as the endpoint of the circle's radius, draw the circle.

11. To inscribe a circle in a triangle:

For triangle ABC, bisect angles < A & < B, extending the bisecting rays so that they intersect. Draw a line perpendicular to line segment AB which goes throught the point where the rays intersect. Taking the point where the rays intersect as the center of the circle and the point where the line perpendicular to AB intersects AB as the end of the circle's radius, draw the circle.

For those interested in constructions in solid geometry, a classic source is Euclid of Alexandria's Elements